Fault Tolerant Message Passing
Principle investigator: Nehal
Desai CCS-1
Co-investigators: Dean Prichard
CCS-1
�������������������� �������� Andrey
Mirtchovski CCS-1
Abstract
Recent trends in the use of
clusters for large scale distributed scientific calculations have moved away
from moderate size clusters of large SMPs, toward very large clusters of
smaller SMPs. With larger numbers of nodes and more complex network topologies,
the issue of reliability becomes paramount. The exponential dependence of the
reliability on the size of the clusters leads to a rapid decrease in the mean
time between failures of the cluster, will render application level reliability
schemes such as checkpoint/restart ineffective.� In this study, we propose to implement a message passing system which
utilizes transparent process mirroring to build a fault tolerant scientific
computing system. Our goal is to increase the usefulness of clusters for
scientific computing by greatly increasing their reliability. This work will
leverage existing work in our group on building message passing systems for a
number of operating systems.
Scientific and Technical Impact of the Proposed Work
This proposal
will address the issue of increasing the reliability of commodity clusters for
scientific computing.� With the
increasing popularity of large scale Beowulf type clusters for scientific
computing come new challenges.� In
addition to the standard challenges of a well performing and scalable cluster
is the issue of reliability.�
Distributed scientific applications are unique among computer
applications because they are extremely intolerant of system failures.� That is, they require all the resources of a
computer (e.g. CPU, network, storage, etc.) at all times.� Therefore, in order for a scientific
calculation to complete properly, system reliability over long periods of time
is a must.� Before we begin any
discussion of reliability, we need to define a few terms:
�
Fault tolerance
is the ability of parallel or distributed systems to recover from component
failures without loss of performance.
�
High availability
(HA) systems provide users with almost uninterrupted services and provide
reduced service during component failure.�
The goal of high availability systems is minimal service interruption,
not fault tolerance.
�
Continuously available
(CA) systems are capable of providing users with uninterrupted services and are
only minimally affected by component or system failures.
In the context
of scientific applications, reliability is equivalent to the level of service provided
by a CA system.
Currently, most
scientific applications rely on checkpointing to provide reliability, but as
the size of clusters grows the effectiveness of the checkpoint-restart paradigm
will diminish.� Because for large
clusters, the mean time between failures (MTBF) of any component may approach
the time required to write/save the data file required to restart the
calculation.� The situation is easily
illustrated by a simple calculation.�
Consider the case of a computer node with a 10000 hour (~1.15 years)
mean time between failures.� With 10000
nodes the probability of all the nodes being up for 1 hour is only 0.5, e.g.
the mean time to failure for the full system is 1 hour.� Functionally, the probability of failure
increases exponentially with the number of nodes.�
The MTBF is the
most generous metric that can be used to estimate system reliability.� In reality, experiences with large-scale
clusters such as ASCI Blue Mountain and ASCI Q show that even a temporary
interruption of any hardware or software component of the cluster environment
will likely cause a scientific application to terminate.� One of the ironies of large-scale clusters
is that as the computing power of the cluster increases the ability to run
large scale distributed scientific codes to completion actually decreases.
For upcoming
tera-scale clusters, the need to incorporate reliability into the design of a
cluster becomes imperative.� For current
large-scale scientific computing clusters, such as the ASCI Q machine, the
estimated MTBF for the full system is on the order of a few hours, compared to
a roughly a day for previous systems such as ASCI Blue Mountain/Pacific.� If current trends continue, the next
generation of large-scale clusters will have MTBF on the order of a few minutes.� For such clusters the checkpoint-restart
methods in current use will be of little help.�
Machines of this scale will require new ways of dealing with this
inherent un-reliability.� This study
proposes to develop techniques to increase the reliability and therefore the
usability of large-scale clusters.�
Background
Increasing the
reliability of computer systems is not a new issue and has been addressed in a
number of different contexts (telecommunications, storage, financial systems,
air traffic control, etc.) using a plethora of different techniques [1,2,6].
Before we
address techniques for increased reliability, we must presume a fault
model.� Faults can be thought as
occurring at various levels in a cluster.�
In this study we assume faults occur at the operational or functional
level.�� Operationally, there are two
sources of unreliability in a computer system: the nodes (CPU) and the
network.� Node faults occur for a number
of reasons including hardware and software failures, and manifest themselves in
a variety of ways from producing incorrect results to total failure.� The other source of unreliability is network
faults, which result from a loss of networking hardware or software.� Network fault tolerance, given its current
commercial importance, has been studied extensively resulting in a number of
distinct methodologies [3].� In this
study, we build and extend, previous work in message passing by implementing a
fault-tolerant routing network.�
In addition to
the source of the faults, fault models make assumptions about the way in which
faults happen or are distributed.� In
the current study, we assume a random fault model, in which components fail
independently.�� This assumption greatly
circumscribes the research, but allows for the introduction of various analytic
modeling techniques.� In the later
stages of this project we hope to remove this assumption, and incorporate more
complex models into the fault tolerance framework.
One of the most
promising methods for dealing with node faults is process mirroring.� In process mirroring, processes used in the
calculation are replicated or mirrored.�
The original and replicated processes are managed as a single unit in
order to maintain identical computation and process state information.� Periodically, information is exchanged
between the replicated processes, allowing a comparison of the calculation and
the detection of faulted nodes.� The
heuristics and algorithms used to determine which information is exchanged and
how to arbitrate the different failure scenarios is key to the effectiveness
process mirroring.� Process mirroring
has been available for commercial purposes such as database and enterprise
resource planning for many years.�
However, to date no one has effectively applied this technique to
distributed scientific computing.
Process units
are of two types: simple and replicated.�
Simple process units are single non-replicated processes.� Replicated units are multiple processes that
are addressed as a single unit. In figure 1, processes 0, 1 and 3 are examples
of simple processes while process 2 is an example of a replicated process.
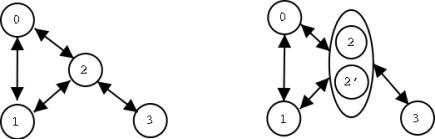
Figure
1: Example of simple (left) and replicated (right) process units.
To understand
the impact that process mirroring has on fault tolerance we need to examine
some basic probability theory.� The
probability of a single node failure as a function of time is given by the
exponential distribution.
�������� p(X>t) = 1 - ebt
where b
can be calculated from the MTBF� as:
b
= -log(1/2)/MTBF
Considering node
failures to be independent events, the probability of having any single node
fail is:
q(t)
= (1 - p(t))n
where n is the
number of nodes.
With process
mirroring the probability of any replicated process unit failing (both
processes in a pair failing) is given by:
q(t)
= (1 - p(t)2)n
where n is the
number of replicated process units.
Figure 2 shows
the example of MTBF = 10000 hrs, and n = 10000 process units.� The left hand panel shows the probability of
success as a function of time without process pairs, while the right hand panel
shows the same results with process pairs.�
It is clear from the figure that replicating processes leads to a huge
improvement in reliability.
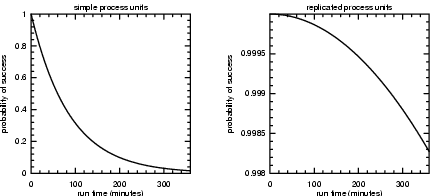
Figure 2: Probability of job success as a function
of job run time, left panel is without process replication, right panel is with
process replication.
Research objectives and goals
The goal of this
study is to increase the usefulness of scientific computing clusters by
increasing their reliability.� Because
of the exponential dependence of the probability of failure on the number of
nodes, increasing system reliability is the key to using commodity clusters to
run tera-scale physics simulations.�
This study will focus on using replicated processes and their extensions
to improve overall machine reliability.�
Increasing the reliability of clusters means users can spend more time
doing science rather than marshaling the checkpoint-restart process.
We propose to
implement a clustering infrastructure, which utilizes process mirroring and
network resiliency to build a fault tolerant continuously available computer
cluster.� This infrastructure will
consist of several components including:
�
The messaging layer which controls the
flow of data between processes.� Since
message passing is the primary mechanism to exchange information in
distributed/parallel scientific computing, much of the reliability will be
implemented at this level.�
�
Autonomous network and node monitoring in
order to determine current hardware and software status.
The messaging
passing component will leverage our previous work in this area [3,5].� Much of the original messaging passing work
in our group was driven by a re-examination of current models of scientific
computation and questions as to whether those models will allow scientist to
fully exploit the ever increasing power of commodity components.� One of the results of these explorations was
the adoption of the Plan 9 operating system [7] as a prototyping/research
environment.� The Plan 9 operating
system is unique and we believe holds great potential for cluster
research.� Plan 9 is appealing for
number of reasons:
�
Plan 9 is a distributed operating system
with a global file system and novel security model.
�
In Plan 9 all system devices are
represented as files. Thus both local and remote resources can be easily
controlled and accessed.� This allows
for the rapid prototyping of new ideas.
�
Support for commodity hardware and
standard network protocols.
�
Operating system support for checkpointing
and process migration.
�
Similar syntax to system V UNIX, allowing
easy porting of applications between plan 9 and traditional Unix systems.
R & D
approach and expected results.��
Phase 1
This phase of
the study will involve adding transparent support for process pairs to our
research messaging system.�� From a
research perspective, the objective is not simply to implement process
mirroring, but to develop to a general framework by:
1. Categorizing
the different failure scenarios.
2. Determining
which scenarios are most likely and should be addressed.
3. Determining
the minimal (and sufficient) set of information that needs to be exchanged
between mirrored processes to allow for detection of various failure scenarios.
4. Constructing
algorithms/heuristics that use this information to avoid the faulty or dead
nodes.
In
addition there are a number of practical considerations, the framework (and its
accompanying infrastructure) must address:�
the availability of resources and the operational needs of users.� In some modes of operation users require
only a high degree of certainty about the accuracy of the calculation and in
others modes they require a high degrees of certainty of job completion.
In
phase 1, all calculation� processes are
mirrored.� Adding complete process
mirroring to an existing distributed calculation results in an increase in the
number of resources required to run a simulation.��� These additional resource requirements must be weighed against
the need to successfully run a simulation (e.g. for mission critical
applications like those in the ASCI program, the choice is obvious).� Figure 3 shows the additional nodes and
network connections needed to implement process replication for a simple grid
communication pattern.
This
increase in resource usage has a large impact on the probability of a distributed
calculation running to completion.� For
example in the case described above, the addition of process replication
increases the probability of the job continuing to run after 1 hour from 0.5 to
greater than 0.99.
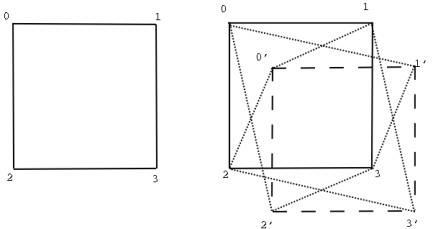
Figure 3: An example of the extra network
connections and mirror nodes required for process replication.
In addition, to the initial fault
tolerant infrastructure we will develop a test suite of representative
application which can be used to demonstrate the effectiveness of the process
replication and the fault tolerant message routing schemes.
Phase 2
While process
replication greatly increases the fault-tolerance of a distributed computing
system, the overhead of mirroring every process maybe too high for some
applications.� In this phase of the
study we will consider replication of only some of the processes.
If f is the
fraction of nodes that have process pairs then the probability of success is
given by:
q(t)
= (1-p(t)2)nf
* (1-p(t))n(1-f)
Figure 4 shows
the probability of success as a function of the fraction of replicated pairs
for run times of 1, 2, 4 and 8 hours.�
One can see that the longer the run time, the more important it becomes
to replicate all processes because of the high probability of failure for the
un-replicated nodes.
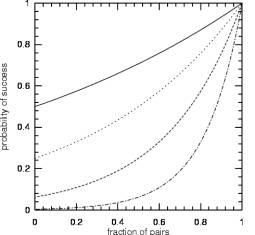
Figure
4: Probability of job success as a function of the fraction of nodes that are
replicated. Solid line is for a run time of 1 hour, dotted is for 2 hours,
dashed is for 4 hours, and dot-dashed is for 8 hour run time.�
We also propose to use information obtained from system monitoring
[4] and the history of the node behavior to estimate which nodes are more
likely to fail in order to determine which processes will be mirrored.� As with Phase 1 we will demonstrate the
software we develop using a test suite of applications on clusters in the ACL
and document the results in a series of reports.
References:
[1] R. Birman,
Spinglass: Adaptive Probabilistic Tools for Advanced Networks http://www.cs.cornell.edu/Info/Projects/Spinglass/
[2] J. Bruck R.
Cypher and C.-T. Ho., Fault-Tolerant Meshes of Hypercubes with Minimal Numbers
of Spares. IEEE Transactions on Computers, 43, 9, 1089-1104. 1991.
[3] R. L.
Graham, M W. Sulalski, L. D. Risinger, D. J. Daniel, N. N. Desai, M. Nochumsen,
and L.-L. Chen, Performance analysis of the LA-MPI communication library. Los
Alamos National Laboratory Technical Report LA-UR-02-1004.
[4]
Ron Minnich and Karen Reid, Supermon: High performance monitoring for Linux
clusters.
The
Fifth Annual Linux Showcase and Conference, Oakland, CA.November 5-10, 2001.
[5] A. A.
Mirtchovski, D. Prichard, and N. N. Desai, Using the Plan9 Operating System in
Cluster Computing For Scientific Applications. Los Alamos National Laboratory
Technical Report. Submitted to Cluster 2002.
[6] P. T.
Murray, R. A. Fleming, P. D. Harry, and P. A. Vickers, Somersault: Enabling
Fault-Tolerant Distributed Software Systems. Hewlett-Packard� Labs Technical Report. HP-98-81, 1998.
[7] R. Pike, D.
Presotto, S. Dorward, B. Flandrena, K. Thompson, H. Trickey, and P.
Winterbottom,� Plan9 from Bell Labs.
Computing Systems, 8(3):221-254, 1995.
Curriculum Vitae
Nehal Desai
Education:
Ph.D��� Mechanical Engineering, North Carolina State University.� Work on multiphasic fluid mechanics.
Relevant Work Experience:
����������� Los Alamos National Lab (Oct 2000-Present)
Technical Staff Member, CCS-1.� Member of Cluster Research Team and� LA-MPI (Los Alamos Message Passing Interface) teams.
����������� IBM (June 1999-Oct. 2000)
Research Programmer.� Advanced Middleware Group.� Worked on several IBM products including:� Personal Communications Manager (PCOMM) and IBM Websphere
�����������
SGI (April 1998-June 1999)
����������� System Engineer for the ASCI BlueMountain System at Los Alamos
����������� Lab.� Part of the BlueMountain integration team.